Lec3_Linear Classification

01. Linear Classification

basic linear function

1-1) Algebraic 관점

1-2) Visual 관점

1-3) Geometric 관점

 

 

 

 

02. Loss function

2-1) L1 Loss

- 실제값과 예측값 사이의 오차의 절댓값 사용

2-2) L2 Loss

- 실제값과 예측값 사이의 오차의 제곱합 사용

2-3) Cross Entropy Loss

2-4) Multiclass SVM Loss

- max가 0이라서 음수를 다룰 수 없는 한계점이 있다. 

 

2-5) Softmax classifier loss

- 위의 SVM loss func을 보완할 수 있는 것이 softmax loss func이다. 

- Softmax Loss function에서는 구한 score값을 exponential 해준 후에 이를 normalization해서 0-1사이의 확률값으로 만들어 사용한다. 

 

 

 

 

 

03. Regularization

 

3-1) Purpose

① Beyond training error : 오버피팅 방지

② Expressing preferences : 본인의 선호도 넣기 위해

③ Prefer simpler models : 좀 더 간단한 모델을 위해

 

 

3-2) Others

• L1 Regularization : 기존 cost function에 가중치의 절댓값을 더해준다.

 

• L2 Regularization : 기존 cost function에 가중치의 제곱을 더해준다.

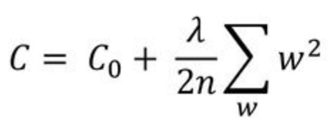
- 원들의 중심이 최소 비용이고, 다이아몬드와 구의 중심이 최소 패널티이다.

- 둘이 만나는 점이 최적의 점이 된다.

- L1 Regularization을 보면 만나는 점이 축 위에 위치해서 가중치 하나가 0이 됨을 알 수 있다. 

이렇게 L1 Regularization은 중요하지 않은 피쳐들의 가중치를 0으로 둠으로써 몇개의 의미있는 피쳐만 사용하고 싶을 때 유용하다.

 

• Elastic Net (L1+L2) : L1규제와 L2규제를 모두 합한 형태

- 변수도 줄이고 싶고, 분산도 줄이고 싶을 때 사용

- 실제 영향을 주는 변수는 A인데, 같이 붙어 다니는 B가 있는 경우, 통계적으로 B도 영향을 주는 것처럼 판단되어

L1만 하면 A가 사라지고 B만 남거나 L2를 하면 beta를 전체적으로 줄여줘서 변수선택이 안되는 문제 발생

 

 

 

• Dropout

- Neural Net의 크기가 커질 경우 Overfitting 문제를 피하기 위한 방법

- 모든 layer에 대해 학습을 수행하는 것이 아니라 입력 layer나 hidden layer의 일부 뉴런을 생략한 신경망을 사용한다.

 -일정한 mini-batch 구간 동안 생략된 망에 대한 학습이 끝나면, 다시 무작위로 다른 뉴런들을 생략(dropout)하면서 반복적으로 학습 수행 -> 보팅 효과 

- co-adaptation(특정 뉴런의 가중치가 큰 값을 가질 때 다른 뉴런들이 제대로 학습하지 못하는 경우)를 피할 수 있다. 

 

 

 

• Batch Normalization : 학습하는 과정 자체를 안정화하여 학습 속도를 가속시킬 수 있는 방법
   

  

  (Motivation) 학습시 레이어를 통과할 때마다 Covariate Shift가 일어나면서 입력의 분포가 약간씩 변해서 학습의 불안정화가 일어난다. 

  (Sol1) Whitening : 각 레이어의 입력의 분산을 평균0, 표준편차1인 입력값으로 정규화 시키는 방법

  _ 하지만 이 방법은 계산량이 많을 뿐만 아니라 편차와 같은 일부 파라미터들의 영향이 무시된다. 

  (Sol2) Batch Normalization : 평균과 분산을 조정하는 과정이 신경망 안에 포함되어 학습 시 평균과 분산을 조정하는 과정 역시 조절된다. 즉 각 레이어마다 정규화 하는 레이어를 두어 변형된 분포가 나오지 않게 조절한다.

  

  + 미니배치의 평균과 분산을 이용하여 정규화 한 뒤에, Scale(감마)와 Shift(배타)값을 통해 실행한다. (비선형 유지에도 도움을 준다.)

   

   

• Cutout : CNN의 입력층 유닛 생략

- cutout에서 생략되는 영역은 개별 픽셀 단위가 아니라, 연속된 영역이다.

- 일부의 특정 표현특성에만 의지하지 않고, 이미지 전체의 컨텍스트를 네트워크가 사용하게 한다. 

- 컴퓨터 비전에서의 object occlusion(두 개이상의 객체가 맞물리는 문제) 해결을 위해서 사용한다. 

 

 

 

• Mixup Regularization

[Related Work]  ERM 기반의 학습 vs VRM 기반의 학습

ERM 기반의 학습 : 주어진 훈련 데이터들을 학습해 모델을 만드는 것 -> OOD(Out of Distribution) 데이터에 취약함.

VRM 기반의 학습 : 훈련 데이터셋의 근방 분포도 함께 활용함 (data augmentation 이용)

 

[수식에서]

(1) 손실함수의 기댓값(=기대위험) 

(2) 경험 분포 정의

여기서 다이락-델타 함수를 이용하는데 이는 (xi,yi)에서만 1이고 나머지 점에서는 0인 함수이다. 

(3) 경험적 기대 위험

(4) 새로운 기대 위험 : VRM기반의 학습으로 확장하여, 훈련 데이터쌍 근방에서 가상의 쌍을 찾을 확률을 재는 근방 분포 

(5) VRM기반의 기대 위험

 

[그림에서]

오른쪽 그림에서 보면 mixup을 이용해서 학습한 결과의 decision boundary가 더 부드럽게 되있음을 알 수 있다.

이는 실제로 mixup이 ERM에 비해서 과적합이 덜 발생하게 되고 regularization 의 역할도 한다고 볼 수 있다. 

 

 

 

• Stochastic depth Normalization : 짧은 네트워크를 훈련하고 테스트 시간에 깊은 네트워크를 사용하기 위한 훈련절차

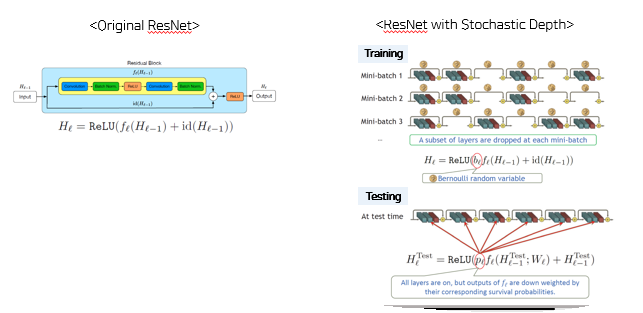
- Dropout 규제는 모델이 깊어지면 규제 기능을 잃어버린다.

- 이에 임의의 확률로 노드를 끄는 Dropout 대신 stochastic depth 방법은 블록 자체를 건너뛰는 방법을 이용한다.

-> 다른 깊이의 네트워크를 가진 모델들 앙상블하는 형태