Abstract
긴 길이를 예측하는 것은 어려움
1) 예측값의 변동성 때문에 2) 계산 복잡도 때문에
그래서
N-HiTS : 새로운 계층적인 보간법과 멀티 비율 데이터 샘플링 기법
-> 예측을 순차적으로 조합하고 다른 주파수로 선택적 강조를 할 수 있게 한다.
실험 결과
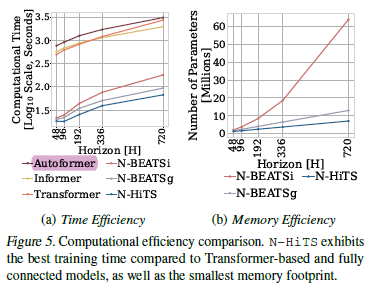
다변량 시계열 예측에서 최근 transformer 모델 대비 25%가 넘는 향상을 보임
1. Introduction
위험관리를 위해 긴 길이의 시계열 예측은 중요하다. ex) 발전소 보수 스케쥴, 인프라 구축 계획, 조기경보 시스템, 헬스케어에서 심박수 등
최근 활발한 연구
1. 예측 모델 발달
attention mechanism // attention-free architecture=fully connected layer들로 구성된 모델
-> 장기 의존성을 잘 파악한다는 특징 BUT 계산 복잡도가 큼
2. multi-step 예측 발달
더 긴 예측을 가능하게 해줌
여전히 문제점 존재
1) 예측값의 변동성 2) 계산 복잡도
Attention과 FCN 모두 O(예측길이의 제곱배)
Contribution
N-BEATS + (multi-rate data sampling을 통해 input 분해) + (multi-scale 보간을 통해 output 합성)
① Multi-Rate Data Sampling
fully-connected block앞에 sub-sampling layer를 포함
-> 계산량 줄이고 장기 의존성 능력은 유지
② Hierachical Interpolation
예측의 차원을 줄이고, multi-scale hierarchical interpolation으로 마지막 output과 시간 규모를 맞춤
-> multi-step 예측을 매끄럽게
③ N-HiTS architecture
input 샘플링의 비율을 계층적으로 합성하는 새로운 방법
-> 시계열 신호의 자신만의 주파수 대역을 예측하는 것으로 각 block을 구체화하여 사용
④ State-of-the-art results
6개의 다변량 시계열 예측에서 SOTA 달성
2. Related Work
▶ Deep time-series forecasting
Autoformer, Informer, Reformer
▶ Multi-step forecasting
① direct multi-step forecast
: 각 timestep마다 다른 모델 적용 -> bias는 작지만 분산이 높음

② joint multi-step forecast
: 한번에 여러 time step 예측, 이전 time step을 예측한 값을 다음 time step을 예측할 때 사용
-> bias와 분산이 균형을 이룸 -> 오류 누적 방지
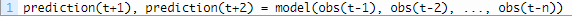
▶ Multi-rate input sampling
mixed data sampling regression (MIDAS) : 파라미터 급증의 문제 완화, 다양한 주파수에서 샘플링된 데이터를 처리
- recursive multi-step forecast 사용

▶ Interpolation
- Interpolation은 신호 및 이미지 처리와 같은 여러 분야에서 모델링된 신호의 해상도를 높이기 위해 광범위하게 사용됨
- 시계열 예측에서, Interpolation은 균형 데이터부터 불균형 데이터에서 까지 모두 사용됨
3. N-HiTS Methodology
- N-BEATS를 장기 시계열 예측에서 더 정확하고 효율적인 계산복잡도를 가지게 확장한 버젼
- 핵심! 입력값의 여러 비율 샘플링 & 예측값의 여러 규모 합성
- 결과! 예측의 계층적 구조, 계산 복잡도 개선, 예측 정확도 향상
MLP - Block - Stack
각 block은 multilayer perceptron (MLP)로 구성됨 - 이는 backcast와 forecast를 위한 계수를 생성
- backcast output은 다음 block의 input을 청소하는데 사용됨
- forecast는 최종 예측값에 합해진다.
이 block들로 stack을 구성 - 각 block들은 각자의 함수로 서로 다른 특징을 구체적으로 학습
3.1. Multi-Rate Signal Sampling
: kernel size k로 MaxPool -> 특정 규모로 input 분석
- 커널 사이즈가 클수록, 고주파/작은 시간 규모를 절단? -> 그 블록은 큰 규모/저주파를 분석
- 이걸 multi-rate signal sampling이라고 부르고, 각 block에 있는 MLP는 서로 다른 샘플링 비율을 사용함.
- 직관적으로, 커널사이즈가 크면 큰 규모 성분 분석 (일관된 장기 예측 결과를 생성하는데 중요함)
- 또한 MLP 입력의 폭을 줄여? 메모리 및 계산 능력 향상, 학습 파라미터 감소시켜 -> 오버피팅 방지
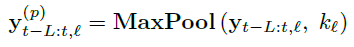
3.2. Non-Linear Regression
: 비선형 forward와 backward를 진행?

3.3. Hierarchical Interpolation
예측의 크기는 horizon H의 차원과 같다. 예를 들어, output embedding H가 커질 수록 encoded input L도 커지는 경향
-> (문제점) 이것은 H가 커질 수록 계산측에서 빠른 inflation을 이끌고 모델이 지나치게 커진다.
그래서
interpolation 사용
-> interpolation coefficient 차원 = 하나의 output time당 파라미터의 개수를 조절하는 expressiveness ratio r


원래 output sampling rate을 회복하고 타겟에서의 H 지점들을 예측하기 위해 보간함수 g를 사용한다.


+ the nearest neighbor, piecewise linear and cubic alternatives. (Appendix A.4.1)
<hierarchical interpolation principle>
: multi-rate sampling으로 합성하는 block들을 거쳐 expressiveness ratios를 분배함으로써 실행
- input에 가까운 block은 작은 r과 큰 k를 가짐 - 이는 더 공격적인 보간을 통해 저순도 신호를 생성
(좀 더 포괄적인, 넓찍한 이라는 의미로 이해)
[순서] 저주파/대규모 -> 고주파/간헐적(세밀)
- 결과 계층적 예측은 / 기본적으로 다른 시간 척도 계층 수준에서 보간으로 구성하면서 / 모든 블록의 출력을 합산함으로써 / 조립된다.

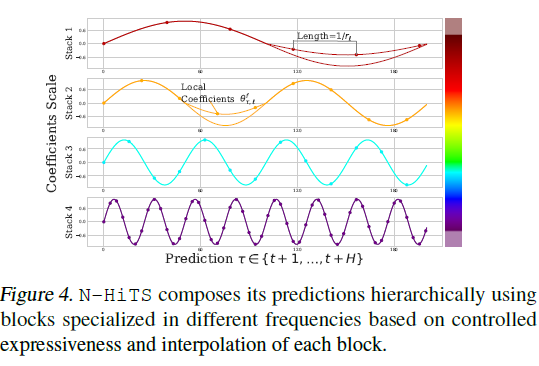
→ 파라미터의 개수를 조절하면서 넓은 주파수대를 다룰 수 있음.
- 마지막으로 backcast residual은 이전 계층 블록이 이미 처리한 대역 외 남은 신호들에 초점을 맞추기 위해 subtract.
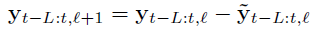
4. Experiment Results

Dataset
Electricity Transformer Temperature, Exchange-Rate, Electricity, San Francisco Bay Area Highway Traffic, Weather, Influenza-like illness
Evaluation setup
MAE, MSE

본 모델은 단변량이므로 자기 변수에 대한 과거 값만 사용
다변량에서는) 각 피쳐들의 예측값을 평가하고 평균냄


(1) kernel pooling size
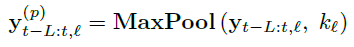
(2) number of coefficients



N-HiTS, our proposed model with both multirate sampling and hierarchical interpolation,
N-HiTS2 only hierarchical interpolation,
N-HiTS3 only multi-rate sampling,
N-HiTS4 no multi-rate sampling or interpolation,
N-BEATSi, the interpreatble version of the N-BEATS
5. Discussion of Findings
✔ 시계열 예측의 맥락에서 발전된 멀티스케일 처리방식을 이용한 연구 필요
❗ 해석가능한 비선형 분해를 제공 -> 추가적인 통찰력 제공, 사용자의 신뢰 향상
✔ expressiveness ratio의 이론적 가이드 필요 ex) Nyquist-Shannon rates
✔ transformer-inspired architecture + integration 방법 연구
'Paper Review' 카테고리의 다른 글
| CoST: Contrastive learning of disentangled seasonal-trend representation for time series forecasting (0) | 2022.04.14 |
|---|---|
| Autoformer (0) | 2022.03.25 |
| Informer (0) | 2022.03.25 |


